Groundwater as a reservoir
Contents
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import panel as pn
pn.extension("katex", "mathjax")
2. Groundwater as a reservoir#
(The contents presented in this section were re-developed principally by Prof. Peter Dietrich and Dr. P. K. Yadav. The original contents are from Prof. Rudolf Liedl)
The content of the previous section was dedicated to very fundamental properties, such as aquifer and its types, solid and liquid (water) volumes in an aquifer, a of subsurface.
In this lecture, the subsurface will be considered from the perspective as a groundwater reservoir and some key definition and parameters will be introduced.
2.1. Groundwater and Aquifers#
If the subterranean water completely fills the pore space we call it groundwater. In Germany a slightly different definition is in use. There, groundwater is only the subterranean water which is not subject to other forces than gravity (see Fig. below). That means, that the water adhesively bound to the grains is not part of the groundwater. Applicable forces in groundwater are sometime locally defined. For, e.g., In Germany the gravity is the only force acting on groundwater, whereas forces such adhesion, cohesion along with gravity are considered internationally.
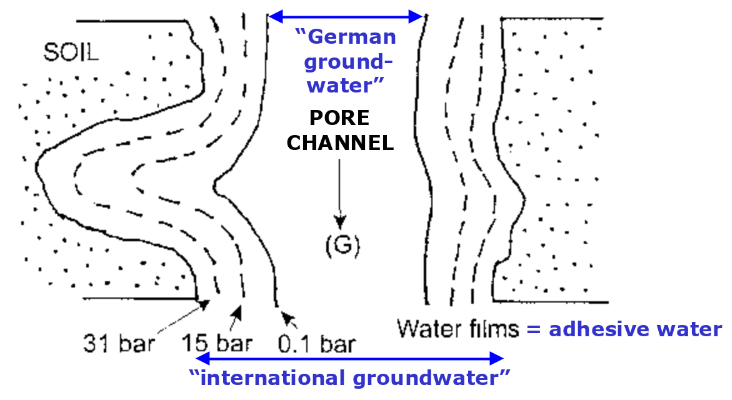
The difference between the international and the German definition of groundwater is the consideration of the adhesive water. Adhesive water does not participate in water movement. The same is true for water in isolated pores or in dead-end pores. All subterranean water not participating in water movement is summarized as immobile water. In contrast, the mobile water is the subterranean water participating in water movement.
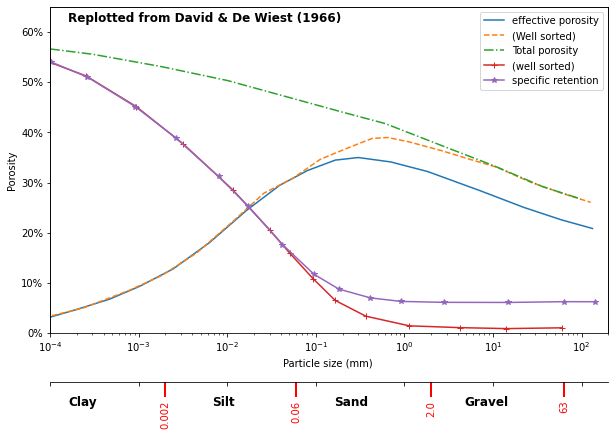
The volumetric share of pore, which can be occupied by mobile water, is termed effective porosity \(n_e\) or flow-through porosity
The effective porosity is dimensionless and the pore volume \(V_{p,m}\) available for mobile water as well as the total volume \(V_T\) has the dimension \(L^3\). Effective porosity cannot exceed total porosity, i.e. \(n_e \leq n\). The difference \((n – n_e)\) is termed specific retention or field capacity. Specific retention is the volumetric share of water which is retained in the porous medium after drainage due to gravitation. The reason for retention is the adhesive force which bounds water at the grain surfaces. Because the available grain surface in a medium depends on the grain size, the effective porosity is also different for various materials. As shown in Figure (below) clay has a high total porosity but only a low effective porosity whereas the total porosity of cobbles is not so significant different from the effective porosity of this material.
2.1.1. Example Problem#
Moist sand specimen = 72.5 cm\(^3\) and its weight = 152 g Oven dried sample = 71.2 cm\(^3\) and its weight = 145 g
Other available information: Specific weight of particles \((\gamma_s)\) = 2.65 g/cm\(^3\) Specific weight of water \((\gamma_w)\) = 1 g/cm\(^3\)
Find, total porosity, void ratio, water content, degree of saturation and effective porosity.
# solution
V_ms = 72.5 # cm^3, volume moist sand
W_ms = 152 # g, weight moist sand, also total volume
V_ds = 71.2 # cm^3, volume dry sand
W_ds = 145 # g, weight dey sand
# Other info
g_s = 2.65 # g/cm^3, sp. weight, particles
g_w = 1 # g/cm^3, sp. wt. water
# intermediate calculation
V_w = (W_ms-W_ds)/g_w # cm^3, W_w/g_w; density = M/V
V_s = W_ds/g_s # cm^3,
V_v = V_ms - V_s # cm^2, volume of voids
W_w = W_ms - W_ds # g, weight of water
# results calculation
n = V_v/V_ms*100 # %, Total porosity
e = V_v/V_s *100 # %, void ratio
w = W_w/W_ds *100 # %, moisture content
S = V_w/V_v * 100 # %, degree of saturation
print("Total porosity is {0:0.2f}%".format(n))
print("Void ratio is {0:0.2f}%".format(e))
print("Moisture content is {0:0.2f}%".format(w))
print("Degree of saturation is {0:0.2f}%".format(S))
Total porosity is 24.53%
Void ratio is 32.50%
Moisture content is 4.83%
Degree of saturation is 39.36%
2.1.2. Example#
Aquifer |
Obs. Point 1 |
Obs. Point 2 |
Obs. Point 3 |
Obs. Point 4 |
|---|---|---|---|---|
A |
— |
— |
Unconfined |
Unconfined |
B |
— |
Unconfined |
Unconfined |
Confined |
C |
Unconfined |
Unconfined |
Confined |
Confined |
D |
Conf./Artesian |
Confined |
Confined |
Confined |
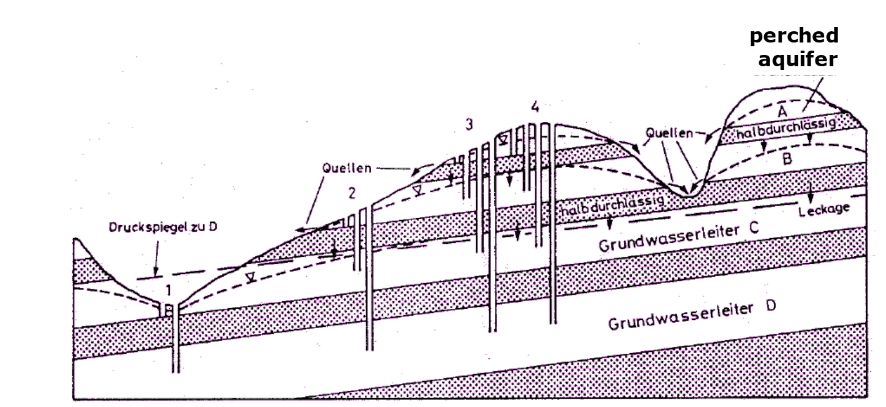
*perched aquifer: Unconfined aquifer on top of another unconfined aquifer, separated from each other by a shallow aquitard
2.2. Pressure and pressure head#
A reason for the movement of groundwater can be (hydrostatic) pressure difference. Let us consider a vertical column containing a porous medium and water filling the voids completely (Fig. below). We can assign to the top an arbitrary reference value pL for the pressure. Due to the load of the overlaying water column, the pressure increase if we go deeper into the column. This is the same as what we observe if we are diving in a lake. The increase of the pressure depends on the density of the fluid and the depth below the water surface. In the setup given in Fig., we have the (hydrostatic) pressure \(p\) [M/L/T\(^2\)] as a function of the height \(z\) [L] above the reference point
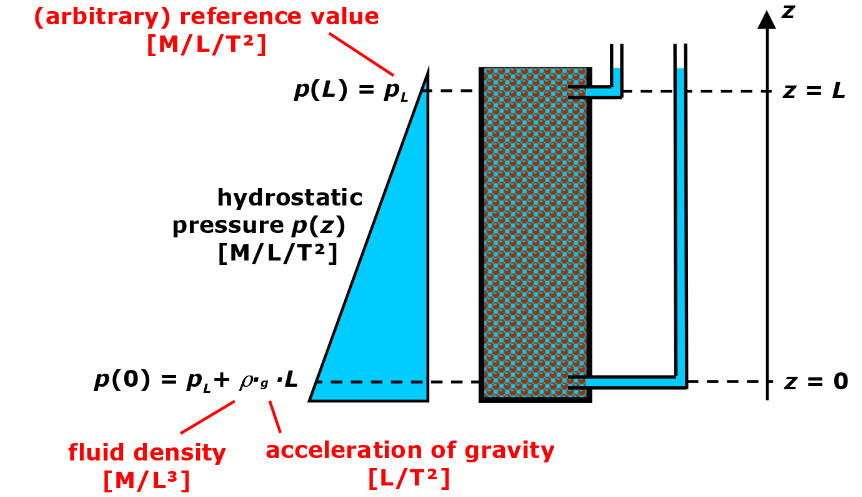
As shown in Fig., we can add two observation points, one at the bottom (\(z = 0\)) and the other at the top of the column \((z=L)\). The pressure difference \(\Delta p\) between the observation points is
Example: Compare the pressure difference for an experimental setup (pipe length 50 cm) in which water and diesel are the two liquids.
# solution
L_p = 50 # cm length of pipe
g = 981 # cm/s^2, accl. due to gravity
# Assume densities
rho_w = 1.0 # g/cm^3, density of water
rho_d = 0.830 # g/cm^3, density of diesel
# calculate
Dp_w = rho_w*g*L_p # g/cm.s^2, pressure difference due to water
Dp_d = rho_d*g*L_p# g/cm.s^2, pressure difference due to water
Dp_w
print("The pressure difference due to water is {0:2.2f} g/cm.s\u00b2,".format(Dp_w),
"and that due to diesel is {0:0.2f} g/cm.s\u00b2.".format(Dp_d), )
The pressure difference due to water is 49050.00 g/cm.s², and that due to diesel is 40711.50 g/cm.s².
2.3. Hydrostatic pressure#
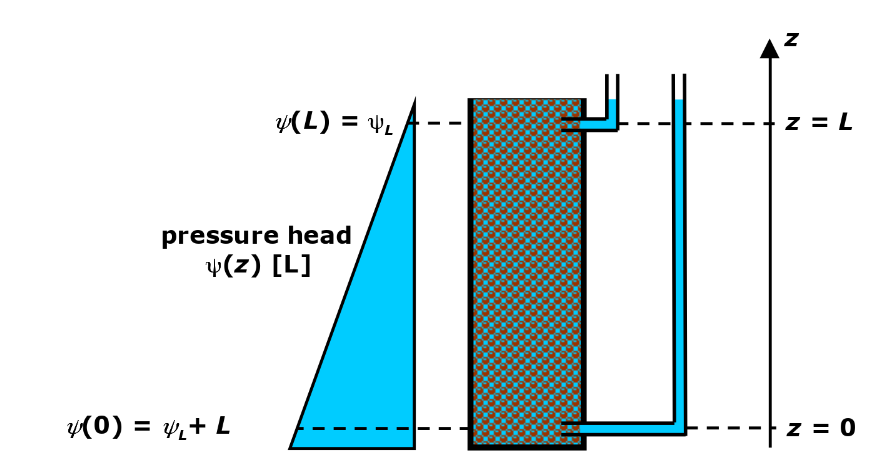
Mostly, pressure head is used instead of pressure when dealing with hydraulic properties or phenomena of the subsurface. The reason is that the pressure head can be easily measured with a tape whereas for a pressure measurement a more expensive manometer is necessary. The (hydrostatic) pressure head \(\psi\) [L] is defined as
This expression makes it clear why we can measure the pressure head with a tape. Similar to pressure head, the hydrostatic pressure can be schematically represented as
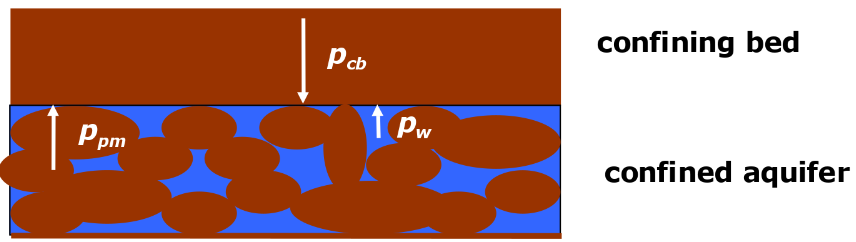
2.4. Pressure in a Confined Aquifer#
Let us now consider a confined aquifer (see Fig. below). The confining bed exerts a certain pressure \(p_{cb}\) on the aquifer. This pressure is compensated partly by the porous medium and partly by the groundwater (pressures \(p_{pm}\) and \(p_w\), respectively). Therefore, we can write the following equation
We can induce a change in the hydrostatic pressure \(\Delta p_w\) with an injection or release of groundwater. According to the above equation we can formulate
The hydrostatic pressure changes do not affect the weight of the confining bed and the exerted downward pressure remains unchanged. Therefore we have
This implies that an increase of hydrostatic pressure automatically results in a decrease in the pressure exerted by the porous medium. In the case of a decrease of hydrostatic the pressure exerted by the porous medium would increase. The change in hydraulic pressure will have two effects with regard to water volume. First, the hydraulic pressure change \(\Delta p_w\) directly leads to expansion/compression of the water and the water volume is accordingly increased/decreased. Secondly, the opposite change \(\Delta p_{pm} = -\Delta p_w\) leads to compression/expansion of the porous medium as a whole (not the individual grains!). This, in turn, results in a reduced/an enlarged pore space such that the stored water volume is decreased/ increased. Both effects contribute to aquifer storage properties (see next section).
2.5. Aquifer storage properties#
Storage properties of the aquifer and associated parameters can be understood by considering pressure changes. For this purpose, we consider the effect of a change in water volume \(\Delta V_w'\) due to a change in hydrostatic pressure. The relative changes in water volume \(\Delta V_w'/\Delta w\) [-] are proportional to change of pressure in groundwater \(\Delta p_w\):
with \(\alpha_w\) as the compressibility of water [LT\(^2\)/M]. The compressibility of water is roughly \(4.4 \cdot 10^{-10}\) m\(^2\)/N. Taking into account an incompressible behavior of the water, that means an increase in hydrostatic pressure results in an inflow of water. A decrease in hydrostatic pressure results would cause an outflow of water. The above equation can be rearranged to yield
With \(\eta\) [-] as the total porosity and \(\Delta \psi\) [L] as the change in pressure head.
2.6. Change in total volume#
The preceding considerations dealt with a change in storage by inflow or outflow. The change was invoked by a change of pressure in groundwater \(\Delta p_w\). But a change could be also invoked by the change of the pressure exerted by the porous medium on the confining layer \(\Delta p_{pm}\). A change \(\Delta p_{pm}\) in the pressure results in a decrease or an increase \(\Delta V_T\) in total aquifer volume. Both quantities are proportional to each other via
whereby the ratio is the relative change of the total volume and \(\alpha_{pm}\) the compressibility of the porous medium [LT\(^2\)/M]. The compressibility of the porous medium is roughly \(10^{-10} - 10^{-8}\) m\(^2\)/N for gravel, \(10^{-9} - 10^{-7}\) m\(^2\)/N for sand, and \(10^{-8} - 10^{-6}\) m\(^2\)/N for clay. Taking into account the relation between pressure and pressure head, the above equation can be rearranged to yield
\(\Delta V_T\) represents a change in volume of the porous medium as a whole. It is composed of a change in volume \(\Delta V_s\) of the solids and another change \(\Delta V_w''\) in water volume. Because the change in volume of the solid is negligible, we can write
If we compare the last two equations we can immediately derive
With words that means a decrease of pressure in the porous medium leads to an expansion of the porous medium and an associated increase in water volume and enlarged pore space. An increase in pressure in the porous medium would lead to a compression of the porous medium and an associated decrease in water volume and reduced pore space.
The total change \(\Delta V_w\) in water volume consists of both effects caused by pressure changes \(\Delta p_{pm}\) and \(\Delta p_w\). Therefore we have
Using the results derived before, we can express how \(\Delta V_w\) depends on changes \(\Delta \psi\) in pressure head
The first term of the sum is related to changes in hydrostatic pressure \((\Delta p_w)\) and the second term to pressure changes in the porous medium \((\Delta p_{pm})\).
Example: The 45 m thick aquifer under the change of pressure 245 KPa compacts 0.20 m. What is the compressibility of porous media.
# Available information
dP = 245 # KPa= KN/m^2, Change pressure
m = 45 # m, aquifer thickness
dm = 0.20 # m, change in aquifer thickness
print("V = A*m and dV = A * dm \n")
# Calculate
al_pm = (dm/m)/dP # m^2/KN, compressibility of porous media.
print("The compressibility of porous media in aquifer {0:0.2e} m\u00b2/KN.".format(al_pm))
V = A*m and dV = A * dm
The compressibility of porous media in aquifer 1.81e-05 m²/KN.
2.7. Specific storage#
For the characterization of the storage properties of an aquifer, we use the term specific storage \(S_s\). It is defined as the volume of water that is released from a unit aquifer volume if hydrostatic pressure head is reduced by one unit
The dimension of specific storage is 1/L. Both impacts on water volume discussed before have to be considered in order to quantify \(\Delta V_w\) in the above equation
The specific storage can therefore also be expressed as
Typical values for specific storage range from \(10^{-6}\) 1/m (e.g. gravel) to \(10^{-2}\) 1/m (e.g. clay).
2.8. Storativity#
Due to their relatively large lateral extent, aquifers are mostly considered as spatially two-dimensional (2D) systems. In this case, specific storage \(S_s\) is replaced by the storativity or storage coefficient \(S\) (Fig. below). Reference volume in a confined aquifer for defining specific storage \(S_s\) is a unit cube (e.g. \(V_T = 1\) m\(^3\)), and for defining storativity \(S\) is a cuboid extending from the aquifer bottom to the aquifer top over a unit area (e.g. \(A = 1\) m\(^2\) and \(V_T = A\cdot m\)).
For confined aquifers \(S\) is simply obtained by multiplying \(S_s\) by the aquifer thickness \(m\)

Storativity can be interpreted as the volume of water released from an aquifer volume extending from the aquifer bottom up to the aquifer top over a unit area if the hydrostatic pressure is reduced by one unit. Storativity is dimensionless.
Actually, unconfined aquifers are always treated as 2D systems. As a consequence, storativity is used to quantify water storage properties. The definition of storativity remains unchanged in principle but the considered aquifer volume now extends from the aquifer bottom up to the water table. For unconfined aquifers, storativity values correspond to effective porosities. This is explained by the free groundwater table. In this case a pressure changes simply lead to filling or emptying of voids. This is fundamentally different from the storage properties of confined aquifers discussed before.
In confined aquifers all voids remain filled with groundwater during pressure changes and storage properties depend on the compressibilities of water and the porous medium.