Tool for simulating 1D Conservative Transport (Laboratory Column)
Contents
7. Tool for simulating 1D Conservative Transport (Laboratory Column)#
Contributed by Ms. Anne Pförtner and Sophie Pförtner. The original concept from Prof. R. Liedl spreasheet code.
7.1. Info on the tool#
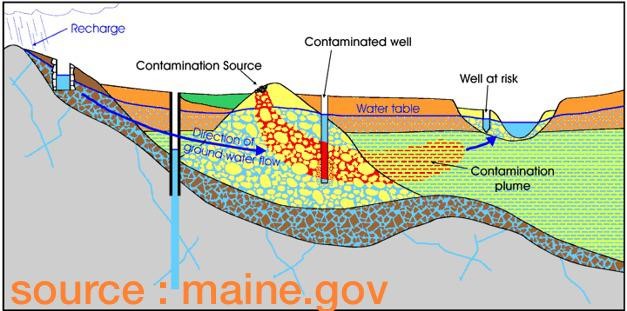
The worksheet addresses 1D conservative transport of a solute through a porous medium, e.g. in a laboratory column.
Water flow through the porous medium is assumed to be steady-state.
Advection and dispersion are considered as transport processes.
Dirac injection, finite pulse injection or continuous injection may be used as upgradient boundary condition.
The worksheet calculates solute breakthrough at the column outlet (sheet “model”) and allows for comparison with measured data (to be provided in sheet “data”).
Computations are based on analytical solutions involving the complementary error function.
input parameters |
dimension |
remarks |
|---|---|---|
column length |
[L] |
enter positive number |
column radius |
[L] |
enter positive number |
effective porosity |
[-] |
enter positive number not bigger than 1 |
dispersivity |
[L] |
enter non-negative number |
flow rate |
[L³/T] |
enter positive number |
initial concentration |
[M/L³] |
enter non-negative number |
input mass |
[M] |
enter positive number or “inf” |
input concentration |
[M/L³] |
enter non-negative number or “inf” |
bulk density |
[M/L³] |
leave empty or enter positive number |
starting time |
[T] |
enter non-negative number |
This tool can also be downloaded and run locally. For that download the _1D_advection_dispersion.ipynb file from the book GitHub site, and execute the process in any editor (e.g., JUPYTER notebook, JUPYTER lab) that is able to read and execute this file-type.
The codes are licensed under CC by 4.0 (use anyways, but acknowledge the original work)
7.1.1. Python Libraries Cell#
numpy for computation, matplotlib.pyplot for plotting and pandas for tabulation, are most general libraries for our works.
ipywidget - for interactive activities, are special functions used in this tool.
Please execute the cell before moving to the next step.
import math
import numpy as np
from ipywidgets import *
import matplotlib.pyplot as plt
7.1.2. Input Data Cell#
In the cell below you can change input values. Pls. read the info above and the table before making the changes the input. Also check the boundary type after executing the cell.
Make sure to execute the cell if you change any input value
#input data
L = 50 #cm, column lenght
R = 3 #cm, column radius
ne = 0.25 #eff. porosity
alpha = 0.1 #dispersivity
Q = 0.167 #cm³/h, flow rate
c0 = 0 #mg/cm³, initital concentration
mi = 2000 #mg, input mass
ci = 1.25e+1 #mg/cm³, input concentration
delta_t = 70 #h, time increment
A = math.pi * R * R #cm², area-cross section
vf = Q/A #cm/h, darcy velocity
va = vf/ne #cm/h, average linear velocity
D = alpha * va #cm²/h, dispersion coeff.
Vp = L/va #pore volume
#intermediate Results
##boundary condition
if mi == math.inf:
print("The type of boundary condition is a continuous injection.")
elif ci == math.inf:
print("The type of boundary condition is a dirac pulse injection.")
else:
print("The type of boundary condition is a finite pulse injection.")
The type of boundary condition is a finite pulse injection.
7.1.3. The main function cell#
You do not have to change the two cells below only have to execute only once.
#Definition of the function
def transport(L, R, ne, alpha, Q, c0, mi, ci, delta_t, t):
A = np.pi * R * R #cm², area-cross section
vf = Q/A #cm/h, darcy velocity
va = vf/ne #cm/h, average linear velocity
D = alpha * va #cm²/h, dispersion coeff.
Vp = L/va #pore volume
##peclet
if alpha == 0:
Pe = np.inf
else:
Pe = L/alpha
##input duration
if mi==np.inf or ci==c0:
ti=np.inf
else:
if ci==np.inf:
ti=0
else:
ti=mi/Q/abs(ci-c0)
Vp = L/va #pore volume
##rel. input duration
if ti == None or Vp == None:
ti_rel = None
else:
if ti == np.inf:
ti_rel = np.inf
else:
ti_rel=ti/Vp
if Vp == None:
delta_t_rel = None
else:
delta_t_rel = delta_t / Vp #rel. time increment
#rel. time
if Vp == None:
t_rel = None
else:
t_rel=t/Vp
##initial condition
###arg-
if Pe == None or t_rel == 0 or Pe == np.inf or t_rel == None:
arg_n1_IC=None
else:
arg_n1_IC=np.sqrt(0.25*Pe/t_rel)*(1-t_rel)
if Pe == None or arg_n1_IC == None or Pe == np.inf or t_rel == 0:
arg_n2_IC = None
else:
if arg_n1_IC > 0:
arg_n2_IC= 1-1*(1-math.erfc(min(abs(arg_n1_IC),27)))
elif arg_n1_IC < 0:
arg_n2_IC= 1+1*(1-math.erfc(min(abs(arg_n1_IC),27)))
else:
arg_n2_IC= 1-0*(1-math.erfc(min(abs(arg_n1_IC),27)))
###arg+
if Pe == None or t_rel == None or Pe == np.inf or t_rel == 0:
arg_p1_IC = None
else:
arg_p1_IC = np.sqrt(0.25*Pe/t_rel)*(1+t_rel)
if Pe == None or arg_p1_IC == None or Pe == np.inf or t_rel == 0:
arg_p2_IC = None
else:
if arg_p1_IC>0:
arg_p2_IC = 1-1*(1-math.erfc(min(abs(arg_p1_IC),27)))
elif arg_p1_IC<0:
arg_p2_IC = 1+1*(1-math.erfc(min(abs(arg_p1_IC),27)))
else:
arg_p2_IC = 1-0*(1-math.erfc(min(abs(arg_p1_IC),27)))
###arg_IC
if Pe == None or arg_n2_IC == None or arg_p2_IC == None or Pe == np.inf or t_rel == 0:
arg_IC = None
else:
if arg_p2_IC == 0:
arg_IC = arg_n2_IC
else:
arg_IC = arg_n2_IC + np.exp(Pe) * arg_p2_IC
##boundary condition
###positive pulse
####arg-
if Pe == np.inf or t_rel==0 or Pe == None or ti_rel == None or t_rel == None or ti_rel == 0:
arg_n1_BC_pp = None
else:
arg_n1_BC_pp = np.sqrt(0.25*Pe/t_rel)*(1-t_rel)
if Pe == None or Pe == np.inf or ti_rel == None or ti_rel == 0 or arg_n1_BC_pp == None or t_rel == 0:
arg_n2_BC_pp = None
else:
if arg_n1_BC_pp>0:
arg_n2_BC_pp = 1-1*(1-math.erfc(min(abs(arg_n1_BC_pp),27)))
elif arg_n1_BC_pp<0:
arg_n2_BC_pp = 1+1*(1-math.erfc(min(abs(arg_n1_BC_pp),27)))
else:
arg_n2_BC_pp = 1-1*(0-math.erfc(min(abs(arg_n1_BC_pp),27)))
####arg+
if Pe == None or Pe == np.inf or ti_rel == None or ti_rel == 0 or t_rel == None or t_rel ==0:
arg_p1_BC_pp = None
else:
arg_p1_BC_pp = np.sqrt(0.25*Pe/ t_rel)*(1+t_rel)
if Pe == None or Pe == np.inf or ti_rel == None or ti_rel == 0 or arg_n1_BC_pp == None or t_rel == 0:
arg_p2_BC_pp = None
else:
arg_p2_BC_pp = math.erfc(min(arg_p1_BC_pp,27))
####arg_BC_pp
if Pe==np.inf or t_rel==0 or Pe==None or ti_rel==None or t_rel==None or ti_rel==0 or arg_n2_BC_pp == None or arg_p2_BC_pp == None :
arg_BC_pp=None
else:
if arg_p2_BC_pp==0:
arg_BC_pp = arg_n2_BC_pp
else:
arg_BC_pp = arg_n2_BC_pp + (np.exp(Pe)*arg_p2_BC_pp)
###negative pulse
####arg-
arg_n1_BC_np=None
arg_n2_BC_np=None
if Pe==None or ti_rel==None or Pe==np.inf or ti_rel==np.inf or ti_rel == 0 or t_rel==0 or t_rel == None:
arg_n1_BC_np = None
else:
if t_rel>ti_rel:
arg_n1_BC_np = np.sqrt(0.25*Pe/(t_rel-ti_rel))*(1-(t_rel-ti_rel))
else:
arg_n1_BC_np = None
if Pe==None or ti_rel==None or arg_n1_BC_np == None or Pe== np.inf or ti_rel==0 or ti_rel == np.inf or t_rel == 0:
arg_n2_BC_np = None
else:
if arg_n1_BC_np > 0:
arg_n2_BC_np = 1-(1-math.erfc(min(abs(arg_n1_BC_np),27)))
elif arg_n1_BC_np < 0:
arg_n2_BC_np = 1+(1-math.erfc(min(abs(arg_n1_BC_np),27)))
else:
arg_n2_BC_np = 1-(0-math.erfc(min(abs(arg_n1_BC_np),27)))
####arg+
if Pe==np.inf or Pe==None or ti_rel==0 or ti_rel==np.inf or t_rel==0 or ti_rel==None or t_rel==None:
arg_p1_BC_np=None
else:
if t_rel>ti_rel:
arg_p1_BC_np=np.sqrt(0.25*Pe/(t_rel-ti_rel))*(1+(t_rel-ti_rel))
else:
arg_p1_BC_np = None
if Pe==None or ti_rel==None or arg_p1_BC_np == None or Pe == np.inf or ti_rel == np.inf or ti_rel == 0 or t_rel ==0:
arg_p2_BC_np = None
else:
if t_rel > ti_rel:
arg_p2_BC_np = math.erfc(min((arg_p1_BC_np),27))
else:
arg_p2_BC_np = None
####arg_BC_np
arg_BC_np = None
if Pe == None or ti_rel == None or arg_n2_BC_np == None or arg_p2_BC_np == None or Pe == np.inf or ti_rel == 0 or ti_rel == np.inf or t_rel == 0:
arg_BC_np = None
else:
if t_rel > ti_rel:
if arg_p2_BC_np == 0:
arg_BC_np = arg_n2_BC_np
else:
arg_BC_np = arg_n2_BC_np+ np.exp(Pe) * arg_p2_BC_np
else:
arg_BC_np = None
##rel conc due initial condition
if Pe == None or t_rel == None:
c_rel_IC = None
else:
if t_rel>0:
if Pe==np.inf:
if t_rel<1:
c_rel_IC = 1
else:
c_rel_IC = 0
else:
c_rel_IC = 1-0.5*arg_IC
else:
c_rel_IC = None
##rel conc due boundary condition
if Pe == None or ti_rel == None or t_rel == None:
c_rel_BC = None
else:
if t_rel > 0:
if Pe == np.inf:
if t_rel > 1:
if ti_rel == np.inf:
if t_rel>1:
c_rel_BC = 1
else:
c_rel_BC = 0
elif t_rel <= 1+ti_rel:
c_rel_BC = 1
else:
c_rel_BC = 0
else:
c_rel_BC = 0
else:
if ti_rel == 0:
c_rel_BC = np.sqrt(0.25/np.pi*Pe/t_rel^3)*np.exp(-0.25*Pe/t_rel*(1-t_rel)^2)
else:
if ti_rel==np.inf or t_rel<=ti_rel:
c_rel_BC = 0.5 * arg_BC_pp
else:
c_rel_BC = 0.5*(arg_BC_pp-arg_BC_np)
else:
c_rel_BC = None
if ti_rel == None or c_rel_IC == None or c_rel_BC == None:
c=None
else:
if t_rel==0:
c=c0
else:
if ti_rel == 0:
c=c0*c_rel_IC+mi/(ne*A*L)*c_rel_BC
else:
c=c0*c_rel_IC+ci*c_rel_BC
return c
7.1.4. The Interactive cell#
Just execute it
def curve_data(L, R, ne, alpha, Q, c0, mi, ci, delta_t, t_max):
plot_c = []
plot_t = np.arange(0, t_max, delta_t)
for t in np.arange(0, t_max, delta_t):
plot_c.append(transport(L, R, ne, alpha, Q, c0, mi, ci, delta_t, t))
return plot_t, plot_c
def plot(L, R, ne, alpha, Q, c0, mi, ci, delta_t, t_max):
plot_t, plot_c = curve_data(L, R, ne, alpha, Q, c0, mi, ci, delta_t, t_max)
plt.plot(plot_t, plot_c)
plt.ylabel('concentration [mg/cm³]')
plt.ylim(-10,30)
plt.xlabel('Time [h]')
plt.xlim(-1, t_max)
plt.show
interact(plot,
L=widgets.FloatSlider(value=50, min=0, max=500, step=1, description='column lenght [cm]:', disabled=False),
R=widgets.FloatSlider(value=3, min=0, max=250, step=0.1, description='column radius [cm]:', disabled=False),
ne= widgets.FloatSlider(value=0.25,min=0, max=1,step=0.05, description='eff. porosity [-]:' , disabled=False),
alpha=widgets.FloatSlider(value=0.1, min=0, max=100, step=0.01, description='dispersivity [cm]:', disabled=False),
Q=widgets.FloatSlider(value=0.167, min=0, max=10, step=0.05, description='flow rate [cm³/h]:', disabled=False),
c0= widgets.FloatSlider(value=0,min=0, max=1000,step=0.5, description='initital concentration [mg/cm³]:', disabled=True),
mi=widgets.FloatSlider(value=2000, min=0, max=10000, step=10, description='input mass [mg]:', disabled=False),
ci=widgets.FloatSlider(value=12.5, min=0, max=1000, step=0.5, description='input concentration [mg/cm³]:', disabled=False),
delta_t= widgets.FloatSlider(value=70,min=0, max=100,step=0.5, description='time increment [h]:' , disabled=False),
t_max = widgets.FloatSlider(value=8400,min=0, max=10000,step=24, description='time [h]:' , disabled=False),
)
<function __main__.plot(L, R, ne, alpha, Q, c0, mi, ci, delta_t, t_max)>